You can watch educational videos I've made on my youtube channel.
News! If you're a student wanting to work with me, please see the following advertisement!
Course Websites
MATH 621, Spring 2019
MATH 321, Fall 2018
MATH 321, Spring 2018
MATH 440/640, Fall 2017
MATH 451/651, Spring 2017
MATH 465/665, Fall 2016
MATH 496/696, Spring 2016
The DARPA Tutorial on Sheaves in Data Analytics MATH 440/640, Fall 2015
MATH 601, Spring 2014
MATH 155, Spring 2014
MATH 540, Fall 2013
MATH 221, Fall 2013
MATH 551, Spring 2013
MATH 560, Fall 2012
MATH 221, Fall 2012
MATH 104, Fall 2011 (Penn)
MATH 104, Fall 2010 (Penn)
MATH 320, Fall 2010 (Penn)
MATH 313, Spring 2009 (Penn)
MATH 114, Fall 2008 (Penn)
Teaching Philosophy
Students are motivated by the relationship between mathematics and the applications where it is most heavily used. In every lecture, recitation, or other meeting with students, I find myself using examples from my own expriences in industry and from science that highlight the use of mathematical concepts and show how they are important. It is of course possible to make progress in any scientific field without a proper understanding of the relevant mathematical theory, but this places one at a significant disadvantage. It is always my experience that knowing a "little more math" results in profoundly improved outcomes, so I encourage my students to try to use course material immediately. I do this by having them engage mathematical concepts in projects that are either realistic or actually used by practitioners in the students' desired field of study. I leverage considerable industry experience in this endeavor, and pride myself on collecting enough data from equipment I have available to create unique and interesting projects.
This last point bears elaboration: since computers have dropped in price substantially, and processor clock speeds have not dramatically changed, manufacturers have added value by adding more extensive sensors to consumer electronics. Many of these sensors are easy to program and yield interesting and compelling datasets on which to build projects. Although I supply the data to the students and assist them with the processing of this data, it is immediately clear to them that "no special widgets" need to be purchased. In particular, all of the projects outlined on this page feature data that was collected on an inexpensive netbook (an Asus EEE 901) or a smartphone (Nokia n900).
I have found that students readily rise to the challenge of learning simple programming in Matlab or GNU Octave without much complaint. My project instructions give them extensive help, and I supply the more challenging (but irrelevant to the course objectives) portions of code. I am willing and excited to spend considerable effort aiding the students in debugging their broken projects. They learn that this doesn't bother me in the least. Ever since I began programming, debugging has always been a favorite activity of mine.
Sample Projects
Audio processing
Here are the sample instructions and data file for this project.
Music and audio signals are especially malleable for the aspiring student. Not only are they fantastically easy to obtain (high-quality, free audio software abounds), they are very convenient to manipulate using Matlab audio file tools. We addressed two specific problems in this project:
- How to extract a (somewhat) hidden harmony from a piece of music, and
- How to compress audio by using a lower sampling rate.
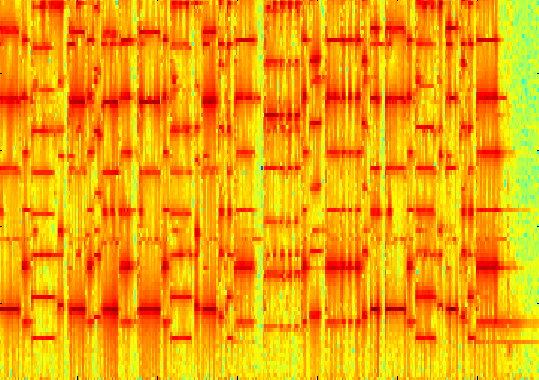
The project consists of a data file containing a violin and cello duet
of a piece of children's music. When the students construct a
windowed FFT of the data, they can visually identify the cello notes
(the bright spots along the bottom of the image) and filter them out
for inspection. The project then asks them to compress this filtered
dataset since it uses substantially lower bandwidth than necessary.
GPS tracking
Here are the sample instructions and data file for this project.
Handheld GPS devices are great fun and very easily available. Many people have them on their phones, and some of these output a running history of where they've been (only on request, one hopes...). Using these GPS tracks, one can do a surprisingly good job of piecing together a story about what the tracked person or object was doing, if good maps are available.
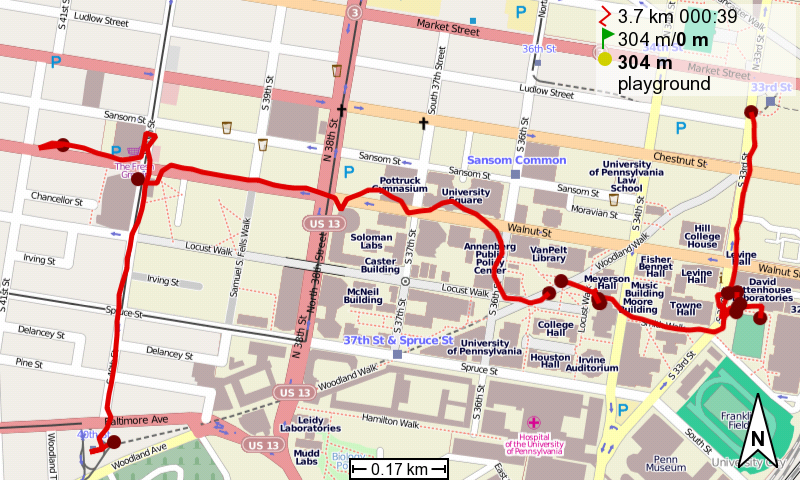
I used the GPS built into my phone to collect a history of
my errands around campus one particularly busy morning. The students
were given a GPX formatted file containing points along the track
shown in the picture at right, which represents where I went. There are a few columns of data in this file, corresponding to the latitude,
longitude, elevation, and time when my GPS recorded my
location.
The students had to use their knowledge of numerical differentiation and integration methods taught in the course to execute the following tasks:
- Determine how far I went in total
- Determine when I was walking, busy inside a building, riding the bus or subway, and
- Determine how far I actually walked (as opposed to taking public transit).
But that isn't quite enough fun! So additionally, I asked the students if they could play the role of "big brother" and figure out exactly what I was doing. For instance, after running my errands, I was quite hungry. Unbeknownst to me, it was still early enough in the day that no restaurants had opened! This caused some moments where I was standing still for no apparent reason, though a little detective work with the timestamps and the hours of nearby establishments could solve this riddle. Additionally, my track actually cuts from the lower left corner of the image to the upper right corner abruptly. All of my students immediately figured out that I had been on the underground trolley!
Computer-aided machining
Here are the sample instructions (no data file) for this project.
Computer controlled machine tools allow complicated shapes to be cut from a block of material with surprising ease. There are lots of types of machine tools out there, some of them pretty complicated. In this project, the students devise some of the instructions for a milling machine. (Incidentally, the first job I ever had was with CNC Software, now Mastercam.com, whose software does just this kind of thing!)
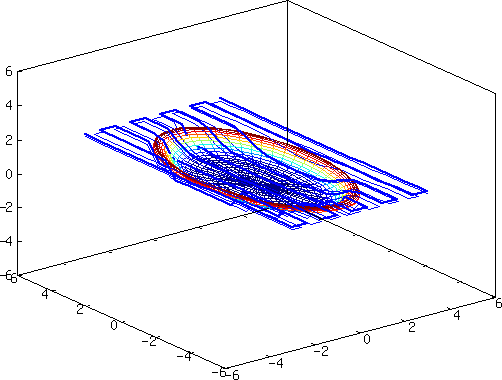
In this project, I gave the students a parametric description of the
surface of an attractive bowl. It is tricky to avoid commanding the tool to accidentally
drill into the object you're machining. This requires an accurate
change of variables from the parametric surface description into the
coordinates where the blade of the tool operates. To make this
conversion, you have to solve a system of nonlinear equations. I
suggested that the students use a multi-dimensional Newton's method,
as we had discussed in class before the assignment of the project.
This task turns out to be fairly intolerant of clerical mistakes (as I found out when writing the project before giving it out to the students), so I supplied the students with separate programs that test their output, essentially unit tests. This encourages the project to be built in modules, and to ensure correctness of each module before attempting to assemble. Of course, this idea isn't the least bit new! I learned it from both industry (where it is extremely common) and from a colleague, Dr. Dietz.