Overview
I am currently pursuing several topics that lie in the intersection of topology with applied mathematics and analysis. One such project stems from my dissertation research, in which I am examining the global behavior of solutions to semilinear parabolic equations with certain polynomial nonlinearities. The primary technique I have been using exploits the similarities and differences of parabolic equations with systems of ordinary differential equations. For instance, a critical point of a parabolic equation whose linearization is stable need not be stable itself. In this case, undestanding the topology of the (infinite dimensional) stable and unstable manifolds for the critical point is essential.
Much of my other work involves the use of algebraic topology to make inroads into difficult signal-processing and imaging problems. For instance, the propagation of the fundamental solution of the wave equation induces a cell complex decomposition of spacetime. This decomposition encapsulates a large amount of information about the topology and geometry of the propagation environment and permits the exploitation of noise-robust, coarse multipath information in mapping and localization.
You can get a presentation outlining my research projects for a quick summary.
Here is the website for the research group at Penn with whom I collaborate.
Ocean wind field measurement
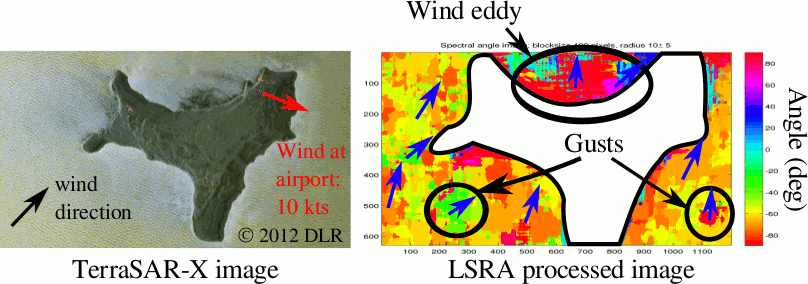
Winds influence the ocean surface in a complicated (and not well-understood) way, which interacts with ocean chemistry, density, and temperature. Understanding the small-scale structure of winds over the ocean surface is critical for understanding the impact of certain rapidly-evolving environmental problems, such as oil spills, algal blooms, and floating debris.
The key factor limiting our understanding of weather patterns over the ocean is low resolution wind data from outdated sensors and overly simplistic analysis methods. The project aims to (1) to acquire experimentally-controlled high-resolution ocean imagery from the German satellite TerraSAR-X, and (2) to develop novel, sophisticated image processing algorithms to analyze the resulting data. Current satellite-borne wind measuring systems give wind measurements spaced 2.5 km apart; our approach should yield similarly accurate measurements a few meters apart, largely due to the availability of higher resolution data products from TerraSAR-X. In order to exploit higher-resolution sensors, new algorithms are required that can measure individual waves. Simply making measurements at a higher resolution is not a viable option; the algorithms currently in use rely on the assumption of low image resolution to ``wash out'' individual ocean swells.
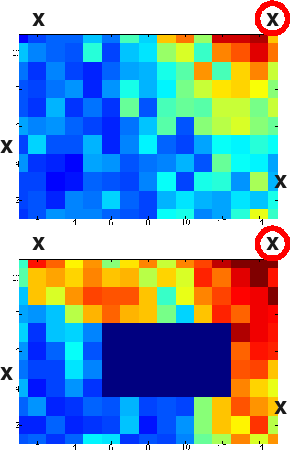
We downloaded the 26 Nov 2012 image of Christmas Island, since swells are visible on the surface of the ocean. In particular, one can see wind direction in surface of the ocean (black arrow on left frame of the picture). This is not typical of SAR images of the ocean, since the wave structure is usually much less apparent. That the wind is blowing strongly with a relatively constant direction is also apparent, since there is a large eddy to the north of the island. Consistent with scatterometry, the pixel radar cross section of the ocean in the eddy is lower than to the south of the island, where the wind is faster.
The right frame of the picture shows the output of our algorithms. The eddy-related effects in the north of the island are readily seen, as well as some "edge effects" around the coast of the island (especially to the south east). These effects are visible in the original image, but are difficult to see: the wind deflects slightly as it flows around the island. Although both of these effects can be validated by examining the original TerraSAR-X image, neither are open-ocean effects. However, two areas to the south east and south west are noticable in the output of our algorithms that have noticeably different wind direction. We believe these are due to the presence of local gusting or calming in those areas, and currently validating them with more extensive experimental data we have collected using TerraSAR-X.
David D'Auria, one of my students, made an excellent video presentation explaining the basics of this project!
Sheaves for signal processing
Signal processing is the discipline of extracting information from related collections of measurements. To be effective, measurements must be organized and then filtered, detected, or transformed in some way to expose the desired information. Distortions from uncertainty and noise oppose these techniques, and degrade the performance of practical signal processing systems. Statistical methods have been developed to ensure consistent performance of these systems, but usually need large amounts of data in aggressively uncertain situations.
A signal consists of a collection of related measurements. Usually, not all of the measurements in a signal are closely related; a given measurement is typically only related to its neighbors in time, space, or frequency. However, most measurements (even those of remote phenomena) are taken locally. Therefore, the appropriate model and subsequent operations on signals should respect the local structure of measurements. The appropriate structure is that of a sheaf, which is a way to assign different kinds of data to each part of a space and to check consistency of this data between neighboring locations.
The signals themselves are rarely the most important feature of a signal processing system. The filters, detectors, and transformations that make up the system are more important. With the more general setting of sheaves over topological spaces, the concept of filters and detectors generalizes as well. I am developing new signal processing systems in which sheaves are the basis of several new and powerful filters, and have a book written on the subject.
Sheaves for networks and asynchronous computation
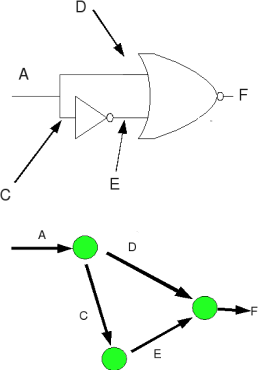
Most digital hardware on the market today is synchronous, which means that it requires a globally-used clock signal. In contrast, asynchronous circuits designed without such a clock can be made more modular, produce less electromagnetic interference, run faster, and consume less power.
Asynchronous logic has been of interest since the earliest days of electronic computing, but owing to the difficulty of designing and debugging it, it is not used much. Some groups, such as Alain Martin's group at Caltech, have built up a repetoire of tools for asynchronous design, but debugging a random asynchronous circuit not designed by their methods is not entirely feasible.
Existing means of debugging asynchronous logic, namely exhaustive time- or event-sampled simuluation or theorem-prover-based methods are computationally expensive, to the point where thorough use on a modern processor would be impossible. I am exploring a different alternatives, namely that of structural analysis. Specifically, I am looking for certain obstructions to proper performance that can be detected by the presence or absence of certain subcircuits. This seems daunting, but it becomes more feasible by working from the bottom up.
Consider the logic states of a single wire. There are only two: one or zero. Inserting a gate between two wires increases the complexity in a specific way, and prevents certain logic states from appearing on certain wires. This is the hallmark of a mathematical object called a sheaf, which as my thesis advisor John Hubbard likes to say is "nothing more and nothing less than a structure for storing local data." Therefore, I have been constructing sheaves that capture aspects of logic circuit behavior, and using the well-established tools of sheaf theory to analyze them, pulling back the results to the circuit's behavior.
Topological Imaging
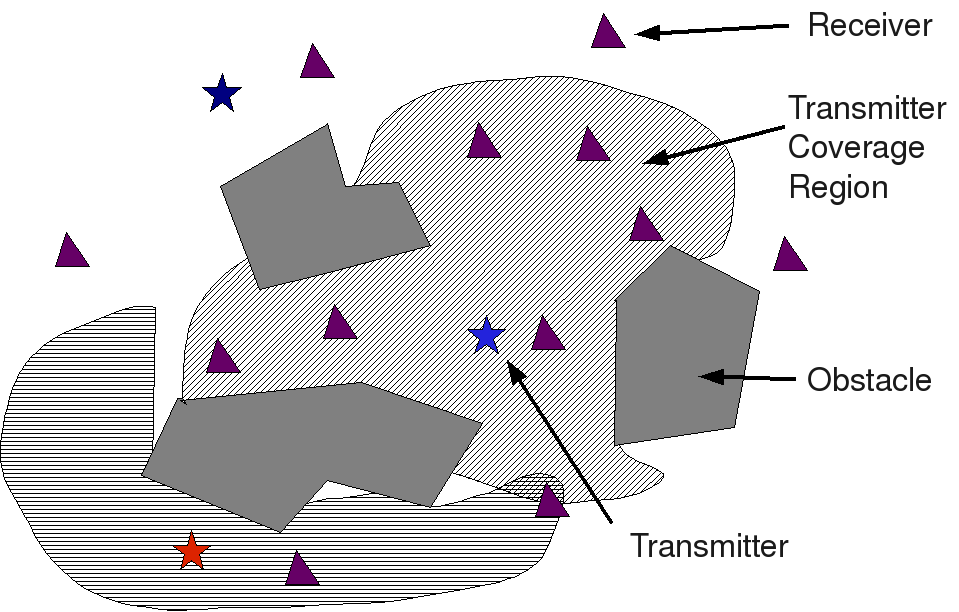
While synthetic aperture imaging has been a technique of choice for constructing information about a domain using controlled wave sources, it suffers from a strong sensitivity to position and timing errors. It would be useful to have a collection of imaging-related techniques that provide graceful degradation in the face of these errors. At the other end of the spectrum from traditional image formation techniques are (yet to be devised) techniques that yield qualitative information about the domain given a random placement of signal transmitter and signal receivers. The topological imaging project aims to develop the underlying theory and algorithms for these methods, and validate them against measurement data.
Theory
At present, there isn't a good theoretical basis for understanding the kind of information that can be obtained when there are substantial position errors. I am working to provide some measure of remedy. It would be very helpful to obtain fundamental bounds for data type and quality, given some desired kind of information as output. For instance, there exist numerous good models of synthetic aperture image focus, signal-to-noise ratio, and the like, given system parameters, collection geometry, and the kind of targets in the scene. In the topological imaging context, of course, the topology of the environment plays a crucial role and needs to be considered.
A similar objective is to develop an understanding of the performance trade-offs between algorithms and their performance. Algorithms will be sensitive to different kinds of geometric and topological errors, so a proper consideration of all of the trade-offs includes both classes of uncertainty. In developing this understanding, I have been working in a framework that appears to be sufficiently general to encompass all known imaging modalities. This also permits me to examine the performance of traditional imaging algorithms in the face of significant multipath in a principled way. Further, the generality of the theory makes specific adjustments to existing algorithms seem natural, and worthy of further exploration.
Finally, I am looking for an obstruction-theoretic way to manage imaging problems. Indeed, a qualitative obstruction can dramatically cut back the space of possible environments in a way that traditional multihypothesis testing approaches to multipath cannot. I have had some notable successes in using the sheaf of local solutions to the Helmholtz wave equation to provide these obstructions.
Algorithms
I am developing new algorithms using this new theoretical framework for imaging. I am specifically interested in algorithms that address the following kinds of problems: those algorithms that operate with
- No knowledge of transmitter or receiver position,
- No knowledge of transmitter position, but single receiver travels a continuous (but unknown path),
- Transmitter(s) and receiver(s) travel continuous (but unknown) paths, and
- Transmitter and receiver colocated along a continuous (but unknown) path.
Experimental data collections
One might ask the following question, "why would a mathematician be involved with collecting experimental data?" It's a valid point, given the unfortunate pure/applied dichotomy in the current field of mathematics. However, only a century ago (not a long time in mathematics), certain mathematicians (for example Charles Babbage) built prototypes, and it was a good thing. Since I have experience with electronics, hardware, software, and the requisite signal processing algorithms, it's actually straightforward to gather measurements to validate my topological algorithms. And it's definitely very fun to do! You can try for yourself by having a look at my demo page!
I am gathering some data in support of testing the algorithms. I am looking to validate existing error models in the theory and suggest new ones. Error models in topological signal processing are a nearly unexplored field, except for the work of Adler, Taylor, and their groups, for instance this paper, by Bobrowski and Borman. And of course, when building anything, you uncover and surmount hidden implementation hurdles, which is always satisfying.
Running these experiments requires very little equipment. Indeed, you need a relatively empty room, (my living room works fine when it's free of childrens' toys), a receiver, and some transmitters. For a receiver, I am using the sound card on my laptop (an Asus EEE 901). I record the audio using Audacity into an uncompressed WAV file, which GNU Octave can read directly. I do all of the offline processing in Octave with some custom-written software. Depending on the experiment, I can also use some of my real-time python code to collect data.

Transmitters are a little more specific to the experiment. I've
custom-made some acoustic sounders for about $15 each. They contain a
programmable microcontroller (a
PIC16F88),
a speaker, a simple audio amplifier, and a control button. They can
be programmed to emit a variety of waveforms, so that the receiver can
discriminate between transmitter signals. Usually, I have them emit
some kind of chirp, the slope of which is selected by the button.
The signal-to-noise ratio from this collection system is surprisingly good, given the low cost of the components. It's good enough for you to see the effects of diffraction and reflection from an obstacle placed in the scene. (See the figure at left. The top frame has no osbtacle, while the bottom frame does. Reflection-induced hot spots are clear above and to the right of the obstacle.)
More details about using computer sound cards to process sonar can be found on my Demonstration page
Euler characteristic integral transforms
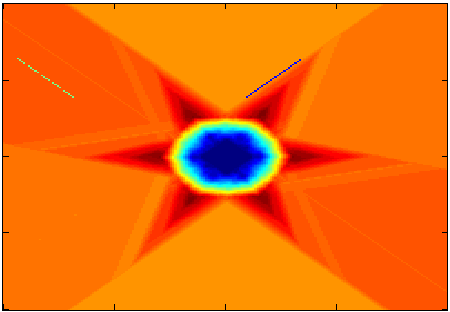
In collaboration with Robert Ghrist, I am studying transforms in the Euler integral calculus. Integral transforms play a central role in signal processing, so our hope is that their analogues in the Euler calculus will also be useful. Already, we have found transforms that are like the Fourier, Bessel, and Haar wavelet transforms. The Fourier and Bessel transforms in Euler calculus both measure width of support of a compactly supported function (as in traditional transform theory), but they also have a particularly elegant index-theoretic formulation. The Bessel transform appears to be helpful for producing measures of centrality for distributions, which fits nicely into the programme of tying the Euler integral calculus to applications in distributed sensing.
Dynamics of semilinear parabolic equations
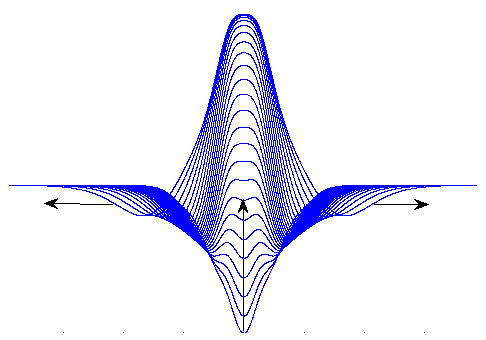
Reaction-diffusion equations are of substantial importance to the understanding of many chemical and biological phenomena. I have been studying the dynamics of a scalar reaction-diffusion equation that arise from adding diffusion and spatial variation to the carrying capacity of the logistic equation. Versions of this kind of semilinear parabolic equation have caught the interest of many different researchers, who usually focus on blow-up conditions and the presence of wave phenomena. My dissertation addressed the presence of bifurcations in the solutions to this equation when the carrying capacity was varied. Under the appropriate conditions, I found that the space of solutions decomposes into a cell complex with finite dimensional cells. Bifurcations amount to attaching or removing cells in a particular way.
In proving this result, I was greatly aided by my discovery of an improved IMEX method for stably computing approximations to solutions, and a new series expansion for equilibria in one spatial dimension.
Future work in this project aims to mimic Floer's construction of a homology theory for Hamiltonian systems by leveraging an important topological index discovered in my dissertation work.
